How would you tokenize (or break down) a million digits of pi?
An exploration into how LLMs tokenize long sequences of numbers and other unusual sequences
A Large Language Model (LLM) needs to break down long sequences of text into shorter “tokens” before it can begin processing them. These tokens comprise a “vocabulary” unique for each model — for example, GPT-4’s vocabulary is 100K while Gemma’s is 256K.

This tokenization process is crucial as it affects how an LLM understands and reasons through an input query. I’ve previously written about how some languages require up to 10x times more tokens than English, resulting in higher costs and longer processing times
In this article, I look into how LLMs process long streams of values. For example:
long strings of numbers (such as a million digits of pi)
repeated numbers (like 0000111122223333)
repeated letters of the alphabet (which might occur in typos, acronyms, or new slang)
For visuals, I used theTokenizer Arena created by Adithya S K to compare the tokenization of multiple models.
A million digits of pi 🍰
First, I examined how LLMs tokenize long numerical sequences. Pi is a good candidate for this, as it is known up to 105 trillion digits. The digits do not follow any discernible pattern and seem random to the naked eye.
GPT-4 and Llama 3 tokenize in groups of 3
Both OpenAI (GPT-4 and the recently released GPT-4o) and Meta’s Llama 3 tokenize the entire numeric sequence in groups of 3. Regardless of what numbers appeared, they were all tokenized in groups of 3.
These groups are arbitrary, in that the order doesn’t really matter. For example, the number [123456] would be tokenized as [123] and [456] while the number 23456 would be tokenized as [234] and [56], which would not capture the relationship between the two numbers (123456 is 100,000 larger than 23456).
Mixtral and Gemma tokenize every single digit
Both open-source models Mistral AI’s Mixtral and Google’s Gemma took a different approach, tokenizing every single digit as its own token.
This means that even a number like “100” is understood by these models as three separate digits: “1”, “0”, and “0”.
Claude’s tokenizer splits up the sequence based on some numeric semantic meaning
Anthropic’s Claude was the most interesting — it tokenized the stream of numbers based on some sort of semantic understanding. Claude’s tokenizer grouped numbers in groups as small as 2 and as large as 7.
For example, the sequence “999999” (which appears in the 762nd digit of pi) is tokenized by the Claude tokenizer as a single token, as is the sequence “222222” (which apparently appears 87 times in the first 100M digits of pi).
The Claude tokenizer also splits up the digits of pi based on 4-digit sequences that look a lot like dates, such as 1988, 1999, and 2020. The top 4-digit tokens in pi are:
How LLMs understand long sequences of numbers depends on its tokenizer
The tokenizers for models like GPT-4 and Llama-3 indiscriminately chunk long streams of numerical digits into groups of 3. The tokenizers for models like Mixtral and Gemma chunk into individual digits. For both of these approaches, it means that each digit (or each group of 3 digits) is its own independent token, regardless of what order they appear in.
The tokenizer for the Claude models seemed to be the exception (at least in the tokenizers tested in this article). It broke up long sequences of numbers based on semantic patterns that may have occurred more frequently in training data, such as repeating digits or numbers akin to 4-digit years.
What surprised me was that none of the LLM tokenizers understood “3.1415” or even “3.14” as its own token. Since pi is used so much in mathematical and engineering problems all over the Internet, I assumed that some truncated representation of it would deserve its own token.
A bit out of scope for this article, but I do think it’s a bit of a miracle that LLMs can do arithmetic at all given that so many of them understand sequences of numbers in arbitrary groups of 3 or individual digits.
Repeated numbers
What if we repeat each number between 0 and 9 a bunch of times? How would the models tokenize that sequence of numbers?
I repeated each digit 32 times and observed the different ways in which the sequence was tokenized.
Just like for the pi sequence, the GPT-4 and Llama tokenizers split up the input sequence into groups of 3, regardless of what digits were included in each group.
Likewise, the tokenizers for the Gemma and Mixtral models tokenized each digit individually.
For Claude, however, the tokenizer split up the sequence using a different approach. 4s came in 4s. 5s sometimes came in 4s and sometimes in 8s. 3s came in groups of 16. Of neighboring digits, 12 and 78 emerged as individual tokens, whereas other neighboring digits (like 23, 34, 45, or 56) did not.
Repeated latin alphabet letters
From digits, I moved on to letters. I took the English alphabet and repeated each (lowercase) letter 32 times.
Some patterns I noticed across the tokenizers:
All letters were tokenized in groups of 2, 4, 8, or 16 (powers of 2)
Sometimes, neighboring characters of two different alphabetic characters would form their own token (like “no”, “uv”, or “sst”)
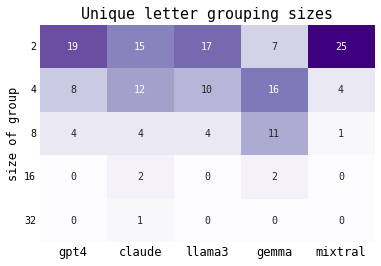
All repeated letters are tokenized in groups of powers of 2
It was no surprise that each LLM tokenized different letters into different sized groups. For example, the GPT-4o tokenizer grouped a long stream of the letter “c” into groups of 4, whereas the Gemma tokenizer grouped the “c”s in groups of 8 and the Claude tokenizer in a single full group of 16.
While these patterns in themselves have little inherent meaning, it is interesting that some of LLMs tokenized more letters in groups of 2 instead of larger groups.
GPT-4o, Claude, Llama 3, and Mixtral tokenizers all grouped repeated letters into groups of 2 more than any other larger group size
Claude and Gemma were the only tokenizers that would group some letters in groups of 16 or 32
Sometimes, neighboring characters of two different alphabetic characters would form their own token
I found that words that occur frequently in LLMs' training data (which is mainly sourced from the Internet and other human-created content like books) were more likely to show up as tokens. The following were the mixed-letter tokens that formed for each of the tokenizers I tested.
gpt4: ab, de, eff, gh, ij, no, op, sst, tu, uv, xy
claude: ab, de, eff, no, op, sst, tu, xy
llama3: ab, de, eff, gh, ij, no, op, sst, tu, uv, xy
gemma: ab, de, eff, gh, hi, ij, st, tu, uv, xy
mixtral: ab, de, eff, gh, ij, no, op, st, tu, uv, xyConcluding remarks
In this article, I examined the tokenizers for several LLMs: GPT-4/4o, Llama 3, Claude, Mixtral, and Gemma. This is by no means a comprehensive list of LLMs or their corresponding tokenizers. The behaviors of tokenizers for other models might mimic those I've shared in this article or deviate entirely from these patterns.
The main takeaway from these experiments is that all tokenizers exhibit unique behaviors when processing unusual input sequences, whether they are long numerical sequences or repetitive characters. This significantly affects how the models understand different kinds of input. LLMs convert human-readable input into tokens, which are then mapped to token IDs. It is within this sequence of token IDs that LLMs learn to discern patterns and "find meaning."
However, the arbitrary nature of tokenization raises questions about how LLMs can effectively "find meaning" in sequences that may or may not have any inherent meaning. The patterns observed in the tokenization of unusual input sequences suggest that the formation of tokens is not always intuitive or easily explainable.
Citation
For attribution in academic contexts or books, please cite this work as
Yennie Jun, "How would you tokenize (or break down) a million digits of pi?," Art Fish Intelligence, 2024.@article{Jun2024tokenizepi,
author = {Yennie Jun},
title = {How would you tokenize (or break down) a million digits of pi?},
journal = {Art Fish Intelligence},
year = {2024},
howpublished = {\url{https://www.artfish.ai/p/how-would-you-tokenize-or-break-down},
}